Egykor engem nem érdekelt a matek. Egy után meg pláne nem. Mégis felkeltette az érdeklődésemet valami. A számoknak több fajtája van, például valós számok és valótlan számok. Természetes számok és természetellenes ill. mesterséges számok. Kerek számok, melyek közül a legkerekebb a nulla.

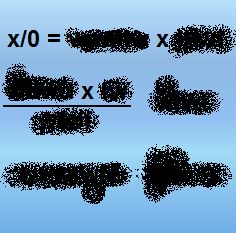
Nagyon bízom benne, hogy megkapom a matematikai Nobel-díjat a legújabb felfedezésemért, ami egyszerűen nélkülözhetetlen a matematikában, annyira alapvető, és a gyakorlati felhasználása is hihetetlenül hézagpótló. Nos, gimiben matekórán anno nem csak az áramkört zárták rövidre és áramszünet lett, hanem a magyarázatot is, hogy mi van akkor, ha gyököt vonunk egy negatív számból. Hatalmas feszültség keletkezik mindenkiben, amikor a mínusz négyből gyököt akarunk vonni, ilyenkor azt mondja a tanár, erre van valami megoldás, de még sincs, és itt muszáj megállni. A pedagógiai gyakorlatban egyértelműen úgy dolgozták ki ezt a tananyagot, hogy ilyenkor történnie kell valaminek. Pl. magyarázat közben hirtelen kicsöngetnek, vagy bombariadó történik, vagy egyéb incidens, pl. belép az igazgató csuromvizes ruhában teljesen idegesen a terembe és kihívja a matektanárt, így muszáj megállnia a magyarázattal. A valószínűségszámítás alapján annak is van minimális esélye, hogy pont akkor, amikor ideér a matektanár a magyarázatban, akkor kezdjen a fal megrepedezni, vagy Neumann képe ilyenkor essen le a falról, vagy egy fekete lyuk ilyenkor közelítse meg a Földet. De általában nem történik semmi. Egyszerűen csak a matektanár leáll itt, és nem mondja el, mi is az a gyökminuszkettő. Nos, nem is a komplex számokat fedeztem fel, hanem valami mást.

A mechanikus számológépek lefagynak, ha nullával kell osztani, végtelen ciklusba kerülnek. Sajnos gyököt vonni nem lehet ezekkel a régi tákolmányokkal, pláne nem negatív számból, pedig jól lefülelhetnénk, mi történik ilyenkor. A lényeg, ezeknek a tákolmányoknak a nullával való osztás és a komplex számok is megfekszik a gyomrukat.

Ahogy nem lehetett beletörődni, hogy ne legyen valami a negatív számok gyökének az eredménye, a nullával való osztásba sem lehet beletörődni, hogy nem értelmezhető. Minél nagyobb számmal osztjuk el X-et, annál kisebb számot kapunk. Ahogy egyre kisebb számmal osztjuk el, mindig egyre nagyobb számot kapunk. Ha pedig eggyel osztjuk el, visszakapjuk önmagát. Ha az osztóval a nulla felé közeledünk, akkor pedig egyre nagyobb a végeredmény. Ha pedig végül a nullával osztjuk el, valami kirobbanóan nagy számot kéne, hogy kapjunk, de nem elég, hogy nagy szám legyen, hanem ezen kívül kell, hogy legyen benne valami plusz. Valami kegyetlenül nagy plusz, valami olyan energia, ami még a nullát is felszorozza egy nullánál nagyobb számra. Ahhoz, hogy a nullát felszorozhassuk, bizonyos meghatározhatatlan, ismeretlen energia kell, vagyis nagyon nagy erő kell hozzá, ez legyen a hipererő. Tehát egy hipererős szám lehet az, amit ha megszorzunk a nullával, nem a nullát kapjuk vissza. Azt a számot, amit ha megszorzunk a nullával és egyet kapunk eredményül, nevezzük HF-nek, ez az angol hyperforce rövidítése. Tehát, ha az egyet elosztjuk nullával, megkapjuk HF-et: 1/0 = 1 HF. Ha a 18-at osztjuk el nullával, 18 HF-et kapunk: 18/0 = 18HF.
Mivel a hipererőt nem ismerjük, elképzelhető, nem annyira egyszerű a dolog, hogy mindössze a hipererő szorzatát kapjuk, ha egynél nagyobb számot osztunk nullával. Nem biztos, hogy 18/0 = 18 HF, hanem a 18 és az egységnyi HF között valami más, eddig ismeretlen műveletet kell végeznünk, vagy akár műveletek sorozatát. Ezt a műveletsorozatot jelöljük egyszerűen [ims]-sel (i=ismeretlen, m=műveletek, s=sorozata). Így tehát 18/0= 18 [ims] HF. Felírhatjuk tehát a képletet:

X/0 = X [ims] HF

Az [ims] és a HF fejtegetéséről legközelebb egy jóval hosszabb bejegyzéssel készülök. A kidolgozással lassan haladok, jelenleg egy word dokumentum 5. oldalánál tartok eddigi fejtegetéseimben. Sajnos elég bonyolult a téma, így lassan haladok vele. Többször átolvastam az eddigieket, ami igazából csak a bevezetője az egésznek, de mindig találok benne valami módosítani valót. Az egyik probléma, hogy a végtelen valahol mindig bepofátlankodik a képbe. Egyszer már úgy nézett ki, sikerült elbánni vele, de máshol újra előbukkant. Más problémák is felmerültek, ezekre egyelőre nem térnék ki, mert túl hosszú levezetések kellenek hozzájuk.

Elvileg lehetséges a komplex és a hipererős számok között műveleteket, pl. szorzást végezni, melyekkel a fekete lyukak egyes tulajdonságainak mértékét határozhatjuk meg.